Test di compressione Strutture a celle fragili stampate in 3D
I ricercatori israeliani Lihi Shenhav e Dov Sherman approfondiscono i test delle strutture cellulari stampate in 3D, delineando le loro scoperte nella recente pubblicazione ” Frattura di fragili strutture a celle aperte stampate in 3D sotto compressione “.
Utili in molte applicazioni a causa del volume, della superficie e del peso, i materiali cellulari vengono utilizzati in parti critiche come celle a combustibile, catalizzatori, scambi di calore e altro; tuttavia, poiché l’ingegneria dei tessuti continua a progredire, vengono anche utilizzati in strutture di ispirazione bio.
“Anticrack” è un termine coniato per quanto riguarda la propagazione delle crepe, come i fenomeni sia biologici che della crosta terrestre. Mentre i materiali sfusi possono presentare propagazione delle crepe a causa di sollecitazioni di trazione, durante la compressione possono verificarsi crepe di materiali porosi che causano problemi come fratture ossee, collassi di edifici, valanghe e altro. Sono state condotte pochissime ricerche sulla propagazione delle crepe sotto compressione, lasciando gli autori motivati a studiare di più sui materiali porosi e sul perché si rompono sotto coercizione.
I ricercatori hanno testato campioni per lo studio costituito da fragili strutture cubiche e tetragonali, con le parti superiori e inferiori composte da due strati stampati in 3D, pensati per sostenere le superfici e prevenire il collasso.
“I campioni cellulari sono caratterizzati da bassa rigidità e carichi applicati. La conformità della macchina di carico è stata valutata utilizzando un campione infinitamente rigido rispetto a quello del campione misurato. Nel nostro caso, è stato scelto un campione di acciaio con le dimensioni del campione di massa “, hanno affermato i ricercatori.
“Gli esperimenti sono stati condotti sotto spostamento controllato in compressione, con_u = 0,1 mm / min. La risposta materiale è stata registrata in termini di carico rispetto allo spostamento. “
I ricercatori hanno stampato in 3D i propri campioni con la stampante 3D HD ProJet500 di 3D Systems. Durante la sperimentazione, è stato applicato un carico per la compressione utilizzando due piastre di alluminio parallele destinate a causare una deformazione uniforme dei campioni, testando quanto segue:
“Le sollecitazioni critiche efficaci e omogeneizzate sotto compressione o, in alternativa, la resistenza a compressione omogeneizzata effettiva, σc eff, ottenuta dal carico critico sull’intera area del campione, sono risultate pari a 1,45 ± 0,13 e 0,99 ± 0,11 MPa per la strutture di cellule cubiche e tetragonali, rispettivamente “, ha affermato il gruppo di ricerca. “Il modulo elastico efficace, E ‘, valutato dalla relazione lineare tra lo stress omogeneizzato e la tensione erano 212,1 ± 27,3 MPa e 193,9 ± 37,4 MPa, rispettivamente, per le strutture cellulari cubiche e tetragonali.
In definitiva, la “struttura di progetto ben ordinata” mostrava una bassa distribuzione delle proprietà misurate e calcolate, con la connessione tra lo stress critico al fallimento dei campioni e lo stress critico che consente il calcolo dei parametri critici. Lo studio ha inoltre dimostrato che quando si verifica la deformazione locale, ciò è dovuto allo stress di compressione, come si vede nella forma con fibbia della colonna in colonne pre-progettate.
“Soprattutto, concludiamo che l’energia della frattura, ~ GIC, dei fragili materiali cellulari sotto compressione non è inequivocabilmente una proprietà materiale, ma dipende dalla geometria di entrambe le colonne e dei campioni. Le proprietà del materiale delle strutture dentellate cellulari sono dettate dal modulo elastico del materiale di base attraverso la teoria della deformazione di Eulero. L’energia della frattura delle strutture rettangolari a celle aperte può essere valutata in modo abbastanza accurato usando pochissimi esperimenti. In pratica, non è necessario valutare l’energia di deformazione vicino alla punta usando il DIC quando si possono ottenere risultati sufficientemente precisi con un metodo più semplice come l’integrale FEA J lungo la superficie libera dell’estrema destra. Infine, le conclusioni di questa ricerca sono applicabili a problemi pratici in diverse discipline e su più scale:
“Infine, le conclusioni di questa ricerca sono applicabili a problemi pratici in diverse discipline e su scale multiple: geofisica (terremoti nella crosta profonda), ingegneria (materiali leggeri all’avanguardia), rischi naturali (valanghe di neve), e, in medicina (ossa umane), tutto di grande interesse per la comunità delle fratture e il campo associato. “

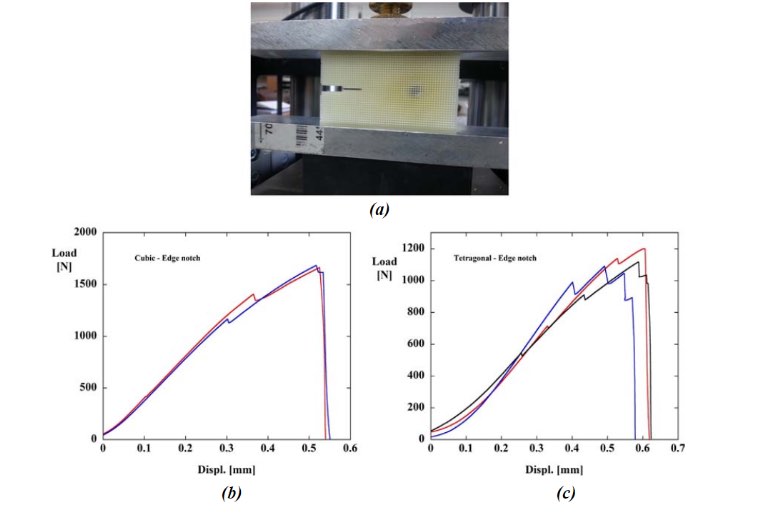
La configurazione sperimentale della frattura e i risultati di campioni di plastica fragili cellulari dentellati: (a) il treno di carico e la relazione carico-spostamento per le strutture cellulari (b) cubiche e (c) tetragonali. In particolare, la colonna sulla punta della tacca è metà dello spessore del resto e, di conseguenza, la caduta di carico iniziale e piccola è associata a un guasto di quella colonna. 
Fotografie ottiche che mostrano i tipi di campione di strutture a celle aperte stampate in 3D: (a) struttura cellulare cubica e (b) struttura cellulare tetragonale, entrambe per valutare le proprietà meccaniche di base. (c) Struttura delle cellule cubiche della tacca del bordo, (d) Struttura delle cellule tetragonali della tacca del bordo, (e) Struttura delle celle cubiche della tacca centrale e (f) Struttura delle cellule tetragonali della tacca centrale per la valutazione delle proprietà e del comportamento della frattura. 
I meccanismi di deformazione e collasso mediante fibbia delle colonne in prossimità della punta dentellata del campione di cellule tetragonali con intaglio centrale (Fig. 1f) sotto compressione: (a) Una vista generale del campione. Si noti che i punti sulla giunzione che fungono da estensimetro virtuale misurano la deformazione di DIC, la tacca a 3 strati lontana dalla punta della tacca e solo una tacca a strato singolo vicino alla punta per evitare il contatto durante la compressione. Nota anche il punto giallo che segna il punto (0; 0) della geometria. (b) La colonna da sinistra a (0; 0) è crollata con un carico relativamente basso poiché il suo spessore è la metà di quello del resto a causa della duplicazione delle cellule durante la tecnica di fabbricazione. (c) Il crollo della prima colonna regolare. Valutazioni della deformazione, deformazione, l’energia di deformazione e l’energia di scissione sono state eseguite dal campo di deformazione appena prima di questo evento, (d) le seconde colonne regolari sono crollate e (e) e (f) mostrano la struttura deformata appena prima e nella fase di pieno collasso. I due pezzi fratturati si sono tradotti in modo significativo l’uno rispetto all’altro dopo la caduta del carico.