Ricerca dell’albero di Monte Carlo: ottimizzazione della pianificazione del percorso utensile nella stampa 3D FDM
Gli autori Chanyeol Yoo, Samuel Lensgraf, Samuel Lensgraf, Lee M. Clemon e Ramgopal Mettu descrivono in dettaglio la loro ricerca per miglioramenti nella stampa 3D FDM, delineata nella recente pubblicazione ” Verso una pianificazione ottimale del percorso FDM con Monte Carlo Tree Search “.
Gran parte della pianificazione del percorso utensile nella stampa 3D FDM consiste in modelli di input suddivisi in livelli; tuttavia, ciò può portare a una mancanza di efficienza in movimento a volte, specialmente quando l’estrusore può ancora essere in movimento ma in realtà non stampa. In questo studio, i ricercatori hanno deciso di calcolare un percorso utensile efficiente e ottimale tramite un nuovo algoritmo utilizzando Monte Carlo Tree Search (MCTS).
“Un potente metodo generico per la navigazione di ampi spazi di ricerca che è garantito per convergere alla soluzione ottimale”, l’MCTS è stato analizzato all’interno di questo studio per quanto riguarda la sua capacità di migliorare le ricerche.
“Per quanto ne sappiamo, questo è il primo algoritmo per la pianificazione del percorso utensile con garanzie sull’ottimalità globale”, hanno affermato i ricercatori.
In precedenza MCTS è stato utile per risolvere i problemi nelle applicazioni di robotica, ottenendo l’efficienza desiderata e maggiore nella pianificazione del percorso utensile.
“L’algoritmo di ricerca dell’albero di Monte Carlo si basa su un algoritmo di ricerca distorto per trovare asintoticamente una soluzione ottimale. A partire da una condizione iniziale, un albero cresce ad ogni iterazione. L’algoritmo trova il prossimo nodo migliore in un albero per espandersi usando il limite di confidenza superiore (UCB), dove UCB si bilancia tra sfruttamento ed esplorazione. Intuitivamente, verrà selezionato il nodo con maggiore probabilità di trovare una soluzione migliore. Una volta selezionato un nodo per l’espansione, una o più sequenze complete vengono generate casualmente dal nodo fino a raggiungere la fine (ad esempio, orizzonte della fine del tempo) “, hanno spiegato gli autori.
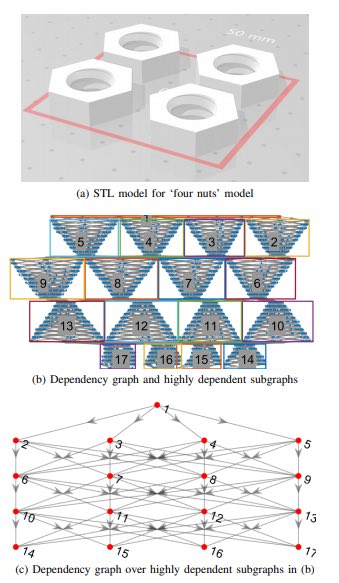
“Per rendere efficiente il nostro algoritmo, introduciamo anche un nuovo algoritmo di clustering sul grafico delle dipendenze per il modello di input.”
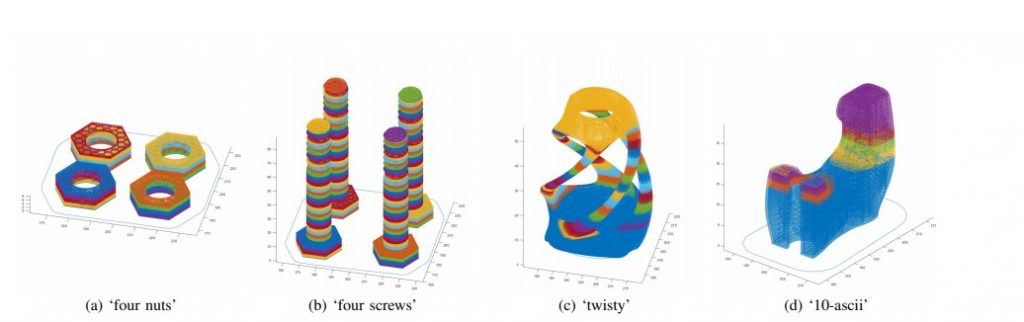
Con un set di dati composto da 75 modelli, l’uso del metodo MCTS ha dimostrato una “riduzione sostanziale” nel movimento sprecato. Gli autori hanno notato che le prestazioni di MCTS erano simili a quelle dell’attuale pianificatore del percorso degli strumenti di ricerca locale, ma nel complesso hanno reso più facile per loro indagare in modo difficile sulla pianificazione con alcuni modelli.
“Una domanda naturale è perché si dovrebbe usare MCTS sulla ricerca locale per un determinato modello. Utilizzando i nostri studi empirici, sembra che l’output della fase di clustering e la successiva composizione dei componenti HDS del grafico delle dipendenze forniscano una guida per stabilire se MCTS può raggiungere la convergenza “, hanno concluso i ricercatori.
“Come abbiamo visto nella nostra analisi empirica se ci sono abbastanza componenti HDS rispetto alla dimensione del grafico delle dipendenze, è molto probabile che MCTS converga in un percorso utensile ottimale. Se il numero di componenti HDS è troppo grande o la dimensione media è troppo piccola, MCTS avrà difficoltà a esplorare lo spazio del percorso utensile e potrebbe comportare risultati peggiori rispetto alla ricerca locale.
“

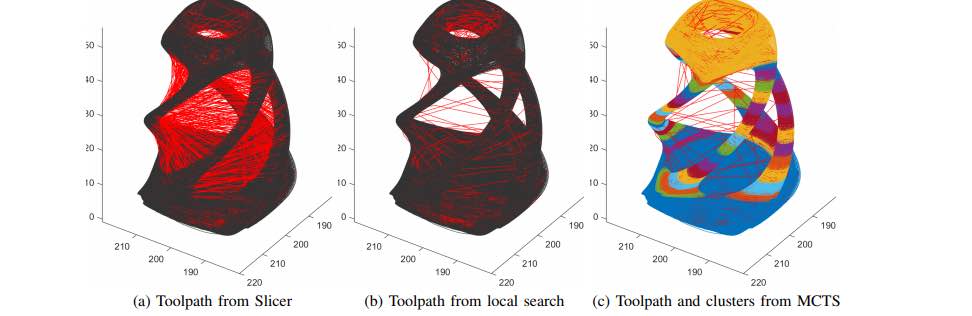
Modello “Twisty”. Percorso utensile per la costruzione della parte mediante (a) tipico pianificatore a strati, (b) ricerca locale da [6] e (c) proposta MCTS, con il rosso che indica il
movimento di non stampa. Il percorso utensile della soluzione per ciascun metodo è mostrato in rosso. Le distanze senza estrusione (in mm) sono rispettivamente 25021, 11423 e 11306.
Modello “Quattro dadi”. Percorso utensile per la costruzione della parte mediante (a) (d) tipico pianificatore a strati, (b) (e) ricerca locale da [6] e (c) (f) proposto MCTS, con il rosso che indica il movimento di non stampa. Il percorso utensile della soluzione per ciascun metodo è mostrato in rosso. Le distanze senza estrusione (in mm) sono rispettivamente 16737, 12220 e 11057. 
Il metodo Monte Carlo è un’ampia classe di metodi computazionali basati sul campionamento casuale per ottenere risultati numerici. Può essere utile per superare i problemi computazionali legati ai test esatti (ad esempio i metodi basati sulla distribuzione binomiale e calcolo combinatorio, che per grandi campioni generano un numero di permutazioni eccessivo).
Il metodo è usato per trarre stime attraverso simulazioni. Si basa su un algoritmo che genera una serie di numeri tra loro non correlati, che seguono la distribuzione di probabilità che si suppone abbia il fenomeno da indagare. La non correlazione tra i numeri è assicurata da un test chi quadrato.
La simulazione Monte Carlo calcola una serie di realizzazioni possibili del fenomeno in esame, con il peso proprio della probabilità di tale evenienza, cercando di esplorare in modo denso tutto lo spazio dei parametri del fenomeno. Una volta calcolato questo campione casuale, la simulazione esegue delle ‘misure’ delle grandezze di interesse su tale campione. La simulazione Monte Carlo è ben eseguita se il valore medio di queste misure sulle realizzazioni del sistema converge al valore vero.
Le sue origini risalgono alla metà degli anni 40 nell’ambito del Progetto Manhattan. I formalizzatori del metodo sono Enrico Fermi, John von Neumann e Stanisław Marcin Ulam[1], il nome Monte Carlo fu inventato in seguito da Nicholas Constantine Metropolis in riferimento al noto casinò situato a Monte Carlo, nel Principato di Monaco, l’uso di tecniche basate sulla selezione di numeri casuali è citato già in un lavoro di Lord Kelvin del 1901 ed in alcuni studi di William Sealy Gosset[1].
L’algoritmo Monte Carlo è un metodo numerico che viene utilizzato per trovare le soluzioni di problemi matematici che possono avere molte variabili e che non possono essere risolti facilmente, per esempio il calcolo integrale. L’efficienza di questo metodo aumenta rispetto agli altri metodi quando la dimensione del problema cresce.
Un primo esempio di utilizzo del metodo Monte Carlo è rappresentato dall’esperimento dell’ago di Buffon e forse il più famoso utilizzo di tale metodo è quello di Enrico Fermi, quando nel 1930 usò un metodo casuale per problemi di trasporto neutronico[1].