MIT: Nuovi algoritmi per la pianificazione dell’estrusione spaziale robotica
Gli scienziati del MIT stanno studiando nuovi modi per migliorare i sistemi automatizzati, delineando le loro scoperte nella recente ” Pianificazione scalabile e probabilisticamente completa dell’estrusione spaziale robotica “. Esplorando nuovi modi per integrare la robotica nella produzione, gli autori hanno creato un nuovo concetto di estrusione spaziale robotica, accompagnato da algoritmi di pianificazione completi.
Concentrandosi su un’alternativa al tradizionale metodo di stratificazione della stampa 3D, i ricercatori hanno cercato di superare le attuali sfide nell’estrusione robotica come la collisione e i vincoli geometrici cinematici, insieme ai vincoli di rigidità. Questo metodo è stato utilizzato solo in misure limitate, che i ricercatori attribuiscono ai vincoli di pianificazione durante build più grandi.
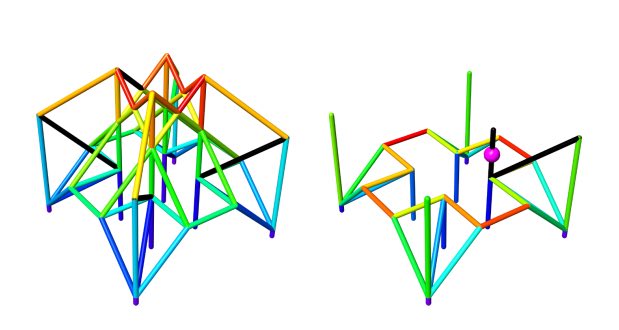
L’algoritmo creato per questo studio si basa su una forma matematica, che consente al team di ricerca di collegare “soddisfacenti vincoli geometrici e strutturali”, poiché la rigidità è inizialmente critica nella costruzione, con le collisioni che limitano le azioni alla fine. Le formule matematiche hanno lo scopo di pianificare sia la rigidità che i vincoli geometrici, “eseguendo globalmente una avida ricerca all’indietro, usando il ragionamento in avanti per orientare la ricerca verso strutture rigide”. Gli scienziati offrono anche l’euristica delle priorità per guidare la rigidità e il processo decisionale geometrico.
Gli scienziati hanno iniziato le formulazioni senza un robot presente, creando una struttura a telaio con un grafico geometrico non orientato hN, Ei incorporato in R 3:
“Lascia che i vertici del grafico N siano chiamati nodi e i bordi del grafico siano chiamati elementi E ⊆ N2 dove m = | E |. Ciascun nodo n ∈ N è il punto di connessione per uno o più elementi nella posizione pn ∈ R 3. Ogni elemento e = {n, n0} ∈ E occupa un volume all’interno di R 3 corrispondente a un cilindro di rivoluzione attorno al segmento di retta pn → pn0. Un sottoinsieme dei nodi G ⊆ N sono rigidamente fissati a terra e quindi subiscono una forza di reazione. “
“Ogni elemento e = {n, n0} può essere estruso da n → n 0 oppure n 0 → n. Lascia che l’elemento diretto ~ e = hn, n0 indichi l’elemento di estrusione e = {n, n0} da n → n 0. Useremo l’insieme P ⊆ E per fare riferimento a un insieme di elementi stampati, che rappresentano una struttura parzialmente estrusa. Sia NP = G ∪ {n, n0 | {n, n0} ∈ P} ⊆ N è l’insieme di nodi distribuiti da nodi di terra G ed elementi P. La pianificazione dell’estrusione richiede innanzitutto di trovare una sequenza di estrusione, un ordine di elementi diretti ψ ~ = [~ e1,…, ~ em] . Useremo ψ per indicare la versione non indirizzata di ψ ~. Lascia che ψ ~ 1: i = [~ e1,…, ~ ei] dia i primi i elementi di ψ ~ dove i ≤ m. ”
La pianificazione dell’estrusione doveva essere completata da un manipolatore robot articolato che aderiva ai limiti articolari ed evitava collisioni con se stesso, l’ambiente e gli articoli appena stampati.
“Consenti a Q: P → Q di essere una funzione che associ un insieme di elementi stampati P ⊆ E allo spazio di configurazione privo di collisioni del robot Q (P) ⊆ Q. Quando non sono stati stampati elementi, Q (∅) è il spazio di configurazione privo di collisioni del robot quando si considerano solo collisioni ambientali, collisioni e limiti articolari. Ogni ulteriore elemento stampato riduce debolmente lo spazio di configurazione senza collisioni … “
Gli autori hanno lavorato su 41 diversi problemi di estrusione in questo studio, con un massimo di 909 elementi e combinazioni degli algoritmi PROGRESSION, FORWARDCHECK e REGRESSION, nonché quattro euristiche: Random, EuclideanDist, GraphDist e StiffPlan. Sono state eseguite quattro prove per ciascun algoritmo, con timeout di un’ora.
PyBullet ha assistito nel controllo delle collisioni, nella cinematica in avanti e nel rendering. Le strutture sono state preelaborate utilizzando una gerarchia di volumi di delimitazione (BVH) con asse statico allineato agli assi (AABB) con ciascun collegamento del robot e quindi sono state utilizzate le seguenti soluzioni:
PLANMOTION utilizzando RRT-Connect
SAMPLEIK usando IKFast
PLANCONSTRAINED utilizzando Randomized Gradient Descent (RGD)
Gli algoritmi PROGRESSION e REGRESSION hanno mostrato prestazioni migliorate, dimostrando che l’euristica ha offerto rigidità e guida geometrica. FORWARDCHECK ha offerto una maggiore precisione per la risoluzione dei problemi rispetto a PROGRESSION, “indicando che è in grado di evitare alcuni vicoli ciechi”. Alla fine, tuttavia, i ricercatori hanno notato che REGRESSION è stato il migliore in termini di confronto con gli altri, brillando sia in termini di successo che di autonomia. Gli algoritmi più performanti hanno risolto il 92 percento dei problemi, con una durata media di circa 15 minuti.
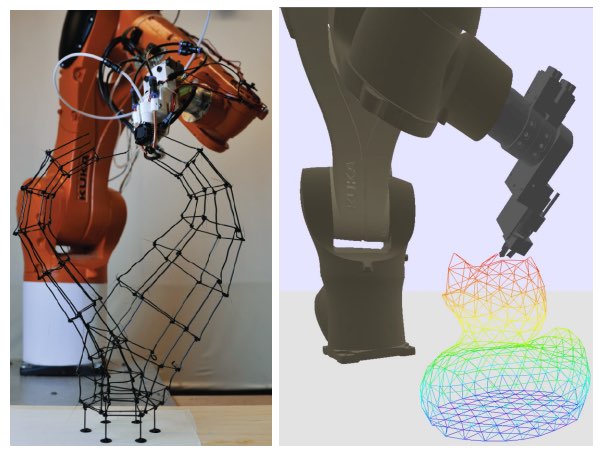
“Abbiamo sperimentato due problemi di estrusione considerati da Choreo. Choreo risolve i problemi “3D Voronoi” e “Topopt beam (piccoli)” in 4025 e 3599 secondi, mentre REGRESSION- EuclideanDist risolve i problemi in 742 e 2032 secondi. Il nostro pianificatore supera Choreo nonostante il fatto che Choreo avesse accesso a informazioni aggiuntive specificate dall’uomo (sezione II). Abbiamo convalidato il nostro approccio su tre problemi di estrusione nel mondo reale. Il più grande dei tre è la bottiglia Klein, che ha impiegato circa 10 minuti per la pianificazione e 6 ore per la stampa.
“Il lavoro futuro prevede l’estensione del nostro approccio alle attività di costruzione per scopi generali”, hanno concluso i ricercatori.
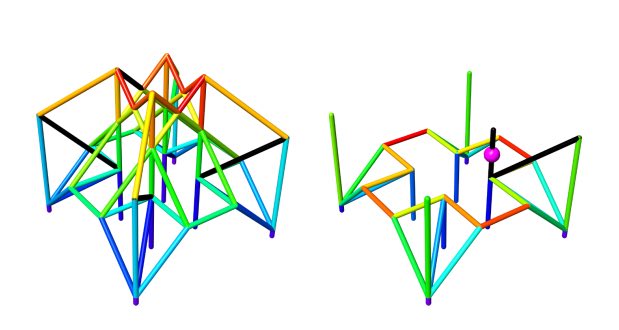
Sinistra: il primo stato in cui PROGRESSION-GraphDist esegue il backtrack (gli elementi neri non sono stampati). A destra: FORWARDCHECK rileva che la stampa dell’elemento indicato dalla sfera rosa impedisce che l’elemento diagonale nero sia estrudibile in modo sicuro. 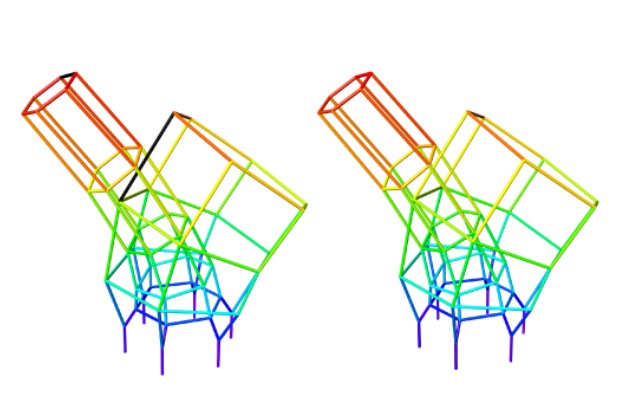
Sinistra: il primo stato in cui PROGRESSION-EuclideanDist fa un passo indietro (gli elementi neri non sono stampati). A destra: REGRESSION-EuclideanDist trova una soluzione senza backtracking. 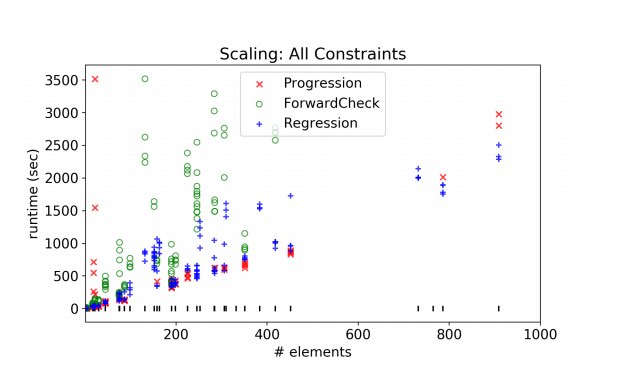
Il runtime di ciascun algoritmo quando si utilizza l’euristica EuclideanDist. I segni di spunta sull’asse x indicano la distribuzione delle dimensioni del problema. 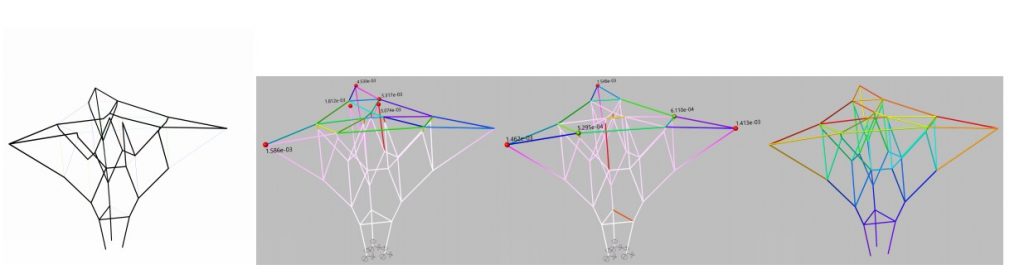
Da sinistra a destra: 1) la sottostruttura non assegnata al primo stato in cui REGRESSION- Random torna indietro. 2) il primo stato in cui REGRESSION- EuclideanDist fa un passo indietro. La deflessione dell’elemento è colorata dal bianco al rosa. I cinque nodi più deformati sono rossi e i loro spostamenti traslazionali sono annotati in metri 3) il primo stato in cui REGRESSION- GraphDist fa un passo indietro 4) REGRESSION- StiffPlan trova una soluzione senza backtracking.